TK
Home

Linear Algebra Fundamentals

• 11 min read
a black background with green dots and linesPhoto by MARIOLA GROBELSKA

This is the second part of the series Mathematics for Machine Learning with Python.

Vectors

What's a vector

A numeric element that has magnitude and direction.

  • magnitude: distance
  • direction: which way is headed

Let's see an example:

v⃗=[21]\begin{equation}\vec{v} = \begin{bmatrix}2 \\ 1 \end{bmatrix}\end{equation}

For this vector, we need to move 2 units in the x dimension and 1 unit in the y dimension. It's a way of saying the directions you need to follow to get to there from here.

import numpy as np
import matplotlib.pyplot as plt

vector = np.array([2, 1])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.quiver(*origin, *vector, scale=10, color='r')
plt.show()

This will plot the vector in the graph:

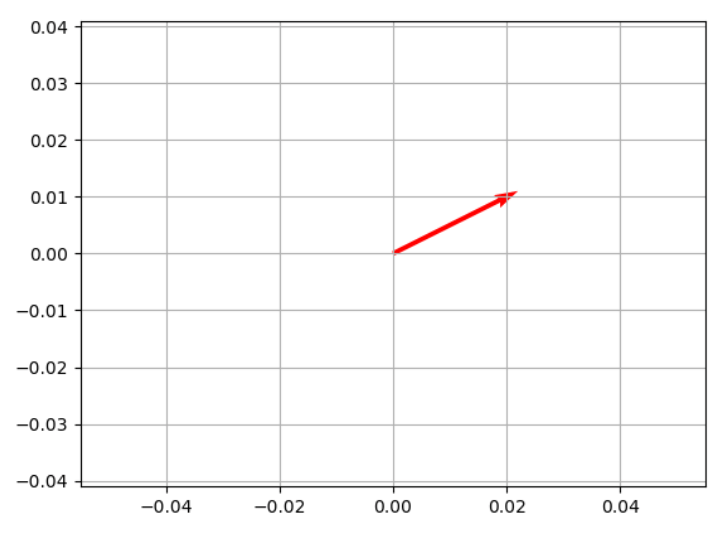
Calculating Magnitude

We can use the Pythagorean theorem and calculate the square root of the sum of the squares.

v = √v₁² + v₂²

For our vector example: v = (2, 1), here's how I calculate it:

v = √2² + 1²
v = √4 + 1
v = √5 ≈ 2.24

In Python, we can use the math module:

import numpy as np
import math

vector = np.array([2, 1])
math.sqrt(vector[0]**2 + vector[1]**2) # 2.23606797749979

Calculating Direction

To calculate the direction (amplitude), we use trigonometry and get the angle of the vector by calculating the inverse tangent tan⁻¹.

tan(𝛉) = 1 / 2
𝛉 = tan⁻¹(0.5) ≈ 26.57°

We can confirm it by calculating it in Python

import math
import numpy as np

v = np.array([2,1])
vTan = v[1] / v[0] # 0.5
vAtan = math.atan(vTan)
math.degrees(vAtan) # 𝛉 = 26.56505117707799

Real Coordinate Spaces

A real coordinate space is all possible real-valued tuples and it's represented with this mathematical symbol

R\mathbb{R}

In linear algebra, we usually see this symbol showing also a number like this:

R2\mathbb{R}^2

In this example, it's called the 2-dimensional real coordinate space, and it represents all possible real-valued 2-tuple. One example is this vector A\textbf{A}:

A=[34]\begin{align*}\textbf{A} &= \begin{bmatrix} 3 \\ 4 \end{bmatrix}\end{align*}

3 is the value for the horizontal axis and 4 for the vertical axis. We can also have different dimensions, like this:

R3\mathbb{R}^3

Following the 2D, this is the 3D real coordinates space:

X=[123]Y=[345]\begin{align*}\textbf{X} &= \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \quad \textbf{Y} &= \begin{bmatrix} 3 \\ 4 \\ 5 \end{bmatrix}\end{align*}

Both are members of the 3-tuple:

X∈RandY∈RX \in \mathbb{R} \quad and \quad Y \in \mathbb{R}

This could increase to an even bigger number. If this number is n, it would call it:

Rn\mathbb{R}^n

The n-dimensional real coordinate space.

Vector Addition

Let's add two vectors:

v⃗=[21]\begin{equation}\vec{v} = \begin{bmatrix}2 \\ 1 \end{bmatrix}\end{equation}
s⃗=[−32]\begin{equation}\vec{s} = \begin{bmatrix}-3 \\ 2 \end{bmatrix}\end{equation}
import numpy as np
import matplotlib.pyplot as plt

v = np.array([2, 1])
s = np.array([-3, 2])

vecs = np.array([v, s])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[0, 0], vecs[0, 1], color=['r', 'b'], scale=10)
plt.quiver(*origin, vecs[1, 0], vecs[1, 1], color=['r', 'b'], scale=10)
plt.show()

Let's calculate the sum of v and s, resulting in z:

z⃗=v⃗+s⃗\begin{equation}\vec{z} = \vec{v}+\vec{s}\end{equation}
z⃗=[21]+[−32]\begin{equation}\vec{z} = \begin{bmatrix}2 \\ 1 \end{bmatrix} + \begin{bmatrix}-3 \\ 2 \end{bmatrix}\end{equation}
z⃗=[21]+[−32]=[−13]\begin{equation}\vec{z} = \begin{bmatrix}2 \\ 1 \end{bmatrix} + \begin{bmatrix}-3 \\ 2 \end{bmatrix} = \begin{bmatrix}-1 \\ 3 \end{bmatrix}\end{equation}

Generate the new vector z with Python:

import numpy as np
import matplotlib.pyplot as plt

v = np.array([2, 1])
s = np.array([-3, 2])
z = v + s

vecs = np.array([v, s, z])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[0, 0], vecs[0, 1], color=['r', 'b'], scale=10)
plt.quiver(*origin, vecs[1, 0], vecs[1, 1], color=['r', 'b'], scale=10)
plt.quiver(*origin, vecs[2, 0], vecs[2, 1], color=['r', 'b'], scale=10)
plt.show()

Here's the plot:

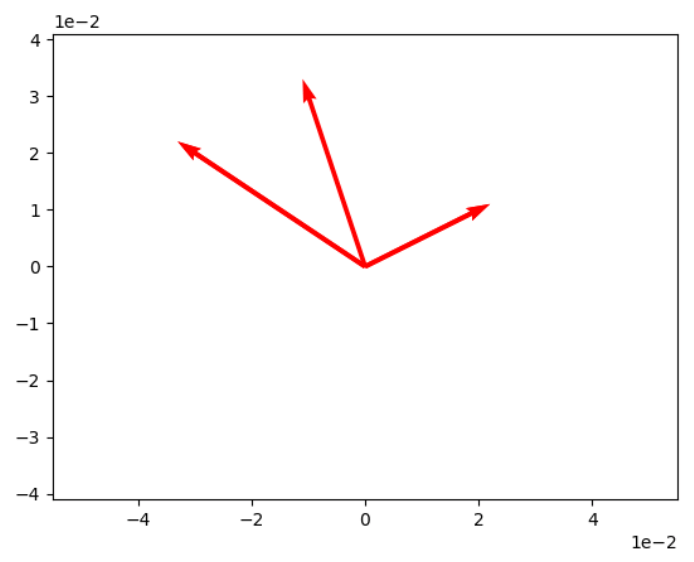
Vector Multiplication

We have 3 ways of performing vector multiplication:

  • Scalar multiplication
  • Dot product multiplication
  • Cross product multiplication

Scalar multiplication is multiplying a vector by a single numeric value.

Let's multiply vector v by 2, resulting in a vector w.

v = (2, 1)
w = 2v

Here's how the multiplication is calculated:

w = (2·2, 2·1)
w = (4, 2)

In Python, we can use numpy to perform the vector multiplication

import numpy as np

v = np.array([2, 1])
w = 2 * v # [4 2]

The magnitude is 2 times longer. One way of thinking about this is that we scale it up by 3.

If we multiply the vector by -1, it won't change its magnitude, but it will change its direction.

The scalar division is the same idea:

import numpy as np

v = np.array([2, 1])
b = v / 2 # [1. 0.5]

In the dot production multiplication, we get the result of two vectors multiplication, in other words, the scalar product (a numeric value).

v·s = (v₁·s₁) + (v₂·s₂) ... + (vₙ·sₙ)

If v = (2, 1) and s = (-3, 2), here's how we calculate the scalar product:

v·s = (2·-3) + (1·2) = -6 + 2 = -4

In Python, we can use the dot method or @ to calculate the scalar product of two vectors.

# using .dot
v = np.array([2, 1])
s = np.array([-3, 2])
np.dot(v, s) # -4

# using @
v = np.array([2, 1])
s = np.array([-3, 2])
v @ s # -4

To get the vector product of multiplying two vectors, we need to calculate the cross product.

v = (2, 3, 1)
s = (1, 2, -2)
r = v·s = ? # vector product

We need to calculate the three components for the final vector:

r₁ = v₂s₃ - v₃s₂
r₂ = v₃s₁ - v₁s₃
r₃ = v₁s₂ - v₂s₁

Here's how we do the calculation in our example:

r = v·s = ((3·-2) - (1·-2), (1·1) - (2·-2), (2·2) - (3·1))
r = v·s = (-8, 5, 1)

In Python, we use the cross method:

p = np.array([2, 3, 1])
q = np.array([1, 2, -2])
r = np.cross(p, q) # [-8  5  1]

Matrices

What's a matrix

A matrix is an array of numbers that are arranged into rows and columns.

A=[123456]\begin{equation}A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \end{equation}

This is how you indicate each element in the matrix:

A=[a1,1a1,2a1,3a2,1a2,2a2,3]\begin{equation}A = \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \end{bmatrix} \end{equation}

In Python, we can define the matrix as a 2-dimensional array:

import numpy as np

A = np.array([[1,2,3],
              [4,5,6]])
# [[1 2 3]
#  [4 5 6]]

To add two matrices of the same size together, just add the corresponding elements in each matrix:

[123456]+[654321]=[777777]\begin{equation}\begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\end{bmatrix}+ \begin{bmatrix}6 & 5 & 4 \\3 & 2 & 1\end{bmatrix} = \begin{bmatrix}7 & 7 & 7 \\7 & 7 & 7\end{bmatrix}\end{equation}

Here's how we calculate it:

A=[a1,1+b1,1a1,2+b1,2a1,3+b1,3a2,1+b2,1a2,2+b2,2a2,3+b2,3]\begin{equation}A = \begin{bmatrix} a_{1,1} + b_{1,1} & a_{1,2} + b_{1,2} & a_{1,3} + b_{1,3} \\ a_{2,1} + b_{2,1} & a_{2,2} + b_{2,2} & a_{2,3} + b_{2,3} \end{bmatrix} \end{equation}

In Python, we can just sum the two matrices:

A = np.array([[1, 2, 3],
              [4, 5, 6]])

B = np.array([[6, 5, 4],
              [3, 2, 1]])

A + B
# [[7 7 7]
# [7 7 7]]

Subtraction of two matrices works the same way:

[123456]−[654321]=[−5−3−1135]\begin{equation}\begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\end{bmatrix}- \begin{bmatrix}6 & 5 & 4 \\3 & 2 & 1\end{bmatrix} = \begin{bmatrix}-5 & -3 & -1 \\1 & 3 & 5\end{bmatrix}\end{equation}

The negative of a matrix is just a matrix with the sign of each element reversed.

C=[−5−3−1135]\begin{equation}C = \begin{bmatrix}-5 & -3 & -1 \\1 & 3 & 5\end{bmatrix}\end{equation}
−C=[531−1−3−5]\begin{equation}-C = \begin{bmatrix}5 & 3 & 1 \\-1 & -3 & -5\end{bmatrix}\end{equation}

In Python, we can use the minus sign:

C = np.array([[-5, -3, -1],
              [1, 3, 5]])
C
# [[-5 -3 -1]
#  [ 1  3  5]]

-C
# [[ 5  3  1]
#  [-1 -3 -5]]

Matrix Transposition is when we switch the orientation of its rows and columns:

[123456]T=[142536]\begin{equation}\begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\end{bmatrix}^{T} = \begin{bmatrix}1 & 4\\2 & 5\\3 & 6 \end{bmatrix}\end{equation}

In Python, we have the T method:

A = np.array([[1, 2, 3],
              [4, 5, 6]])
A.T
# [[1 4]
#  [2 5]
#  [3 6]]

Matrix Multiplication

Scalar multiplication in matrices looks similar to scalar multiplication in vectors. To multiply a matrix by a scalar value, you just multiply each element by the scalar to produce a new matrix:

2×[123456]=[24681012]\begin{equation}2 \times \begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\end{bmatrix} = \begin{bmatrix}2 & 4 & 6 \\8 & 10 & 12\end{bmatrix}\end{equation}

In Python, we simply perform the multiplication of two values:

A = np.array([[1,2,3],
              [4,5,6]])

2 * A
# [[ 2  4  6]
#  [ 8 10 12]]

To multiply two matrices, we need to calculate the dot product of rows and columns.

[123456]⋅[987654]\begin{equation}\begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\end{bmatrix} \cdot \begin{bmatrix}9 & 8 \\ 7 & 6 \\ 5 & 4\end{bmatrix}\end{equation}

How to calculate this multiplication:

  • First row from A times first column from B = First row, first column
  • First row from A times second column from B = First row, second column
  • Second row from A times first column from B = Second row, first column
  • Second row from A times second column from B = Second row, second column

Resulting in these calculations:

(1·9) + (2·7) + (3·5) = 38
(1·8) + (2·6) + (3·4) = 32
(4·9) + (5·7) + (6·5) = 101
(4·8) + (5·6) + (6·4) = 86

Resulting in this matrix:

[383210186]\begin{equation}\begin{bmatrix}38 & 32\\101 & 86\end{bmatrix} \end{equation}

In Python, we can use the dot method or @:

import numpy as np

A = np.array([[1, 2, 3],
              [4, 5, 6]])

B = np.array([[9, 8],
              [7, 6],
              [5, 4]])

np.dot(A,B)
A @ B
# [[ 38  32]
#  [101  86]]

For matrix multiplication, we commutative law doesn't apply:

A = np.array([[2, 4],
              [6, 8]])

B = np.array([[1, 3],
              [5, 7]])

A @ B
# [[22 34]
#  [46 74]]

B @ A
# [[20 28]
#  [52 76]]

Identity matrices are matrices that have the value 1 in the diagonal positions and 0 in the rest of the other positions.

An example:

[100010001]\begin{equation}\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix} \end{equation}

Multiplying a matrix by an identity matrix results in the same matrix. It's like multiplying by 1.

[123456789]⋅[100010001]=[123456789]\begin{equation}\begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\\7 & 8 & 9\end{bmatrix} \cdot \begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix} = \begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6\\7 & 8 & 9\end{bmatrix} \end{equation}

Matrix Division

Matrix division is basically multiplying it by the inverse of the matrix

A÷B=A⋅B−1A \div B = A \cdot B^{-1}

How the inverse of a matrix is calculated? Using this equation:

[abcd]−1=1ad−bc[d−b−ca]\begin{equation}\begin{bmatrix}a & b\\c & d\end{bmatrix}^{-1} = \frac{1}{ad-bc} \begin{bmatrix}d & -b\\-c & a\end{bmatrix}\end{equation}

Let's see it in action:

[6212]−1=[0.2−0.2−0.10.6]\begin{equation}\begin{bmatrix}6 & 2\\1 & 2\end{bmatrix}^{-1} = \begin{bmatrix}0.2 & -0.2\\-0.1 & 0.6\end{bmatrix}\end{equation}

In Python, we can use the linalg.inv method:

import numpy as np

B = np.array([[6, 2],
              [1, 2]])

np.linalg.inv(B)
# [[ 0.2 -0.2]
#  [-0.1  0.6]]

Larger matrices than 2x2 are more complex to calculate the inverse, but it is calculated in the same way in Python:

B = np.array([[4, 2, 2],
              [6, 2, 4],
              [2, 2, 8]])

np.linalg.inv(B)
# [[-0.25   0.375 -0.125]
#  [ 1.25  -0.875  0.125]
#  [-0.25   0.125  0.125]]

With the calculation of the inverse, we can now calculate the multiplication of a matrix with an inverse of another matrix.

[1234]⋅[6212]−1\begin{equation}\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} \cdot \begin{bmatrix}6 & 2\\1 & 2\end{bmatrix}^{-1} \end{equation}
=[1234]⋅[0.2−0.2−0.10.6]\begin{equation}=\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} \cdot \begin{bmatrix}0.2 & -0.2\\-0.1 & 0.6\end{bmatrix} \end{equation}
=[(1×0.2)+(2×−0.1)(1×−0.2)+(2×0.6)(3×0.2)+(4×−0.1)(3×−0.2)+(4×0.6)]\begin{equation}=\begin{bmatrix}(1\times0.2)+(2\times-0.1) & (1\times-0.2)+(2\times0.6)\\(3\times0.2)+(4\times-0.1) & (3\times-0.2)+(4\times0.6)\end{bmatrix}\end{equation}
=[010.21.8]\begin{equation}=\begin{bmatrix}0 & 1\\0.2 & 1.8\end{bmatrix}\end{equation}

In Python, we can just invert the matrix and multiply by the inverse:

A = np.array([[1,2],
              [3,4]])

B = np.array([[6,2],
              [1,2]])

A @ np.linalg.inv(B)
# [[0.  1. ]
#  [0.2 1.8]]

Systems of Equations

We can write a system of equations in matrix form. Take a look a these equations:

2x+4y=18\begin{equation}2x + 4y = 18\end{equation}
6x+2y=34\begin{equation}6x + 2y = 34\end{equation}

We can write this in matrix form:

[2462]⋅[xy]=[1834]\begin{equation}\begin{bmatrix}2 & 4\\6 & 2\end{bmatrix} \cdot \begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}18\\34\end{bmatrix}\end{equation}

And we can write this in another way:

A=[2462]        X=[xy]        B=[1834]\begin{equation}A=\begin{bmatrix}2 & 4\\6 & 2\end{bmatrix}\;\;\;\;X=\begin{bmatrix}x\\y\end{bmatrix}\;\;\;\;B=\begin{bmatrix}18\\34\end{bmatrix}\end{equation}

We know that A · X = B, which is the same as B ÷ A = X, which is the same as B · A⁻¹ = X.

The inverse of A is:

A−1=[−0.10.20.3−0.1]\begin{equation}A^{-1} = \begin{bmatrix}-0.1 & 0.2\\0.3 & -0.1\end{bmatrix}\end{equation}

So:

X=[−0.10.20.3−0.1]⋅[1834]\begin{equation}X = \begin{bmatrix}-0.1 & 0.2\\0.3 & -0.1\end{bmatrix} \cdot \begin{bmatrix}18\\34\end{bmatrix}\end{equation}

The result of the matrix X is

X=[52]\begin{equation}X = \begin{bmatrix}5\\2\end{bmatrix}\end{equation}

In Python, we can confirm that:

A = np.array([[2, 4],
              [6, 2]])

B = np.array([[18],
              [34]])

X = np.linalg.inv(A) @ B
# [[5.]
#  [2.]]

Resources

Hey! You may like this newsletter if you're enjoying this blog. ❤
✖

Twitter · Github