Building A Deep Neural Network from Scratch

Photo by Zach Lezniewicz

In the last post, I wrote about how a neural network works under the hood, from math to code, from theory to Python. The post talked about how to build a simple neural net, also called a shallow neural network because it has only one hidden layer (together with the input and the output layers).

In this post, I plan to build upon that first implementation of a shallow neural net and transform it into a deep neural net. The first idea is to just increase the neural net in one layer to see how it behaves, and then abstract it into a reusable class, and make it easy to pass the number of layers and hidden units per layer and the model figures out how to build on top of that.

Adding more layers and hidden units to the neural net increases the complexity of the model and so we need to understand other topics like input normalization, vanishing and exploding gradients, regularization, mini-batches, and other interesting concepts so we can make the deep neural net perform better on the dataset problem.

Adding one layer

To revisit the previous implementation of the shallow neural network, take a look at the previous blog post and the neural net implementation on github. This first part and most of this post will work on top of that implementation with a few tweaks and changes.

To add a new hidden layer, we need a few changes in the code:

• Add parameters $W$ and $B$ for the new layer
• Compute $Z^{[1]}$ and $A^{[2]}$ in the forward propagation ($Z^{[3]}$ and $A^{[3]}$ will be computed for the output layer with the softmax)
• Compute $dZ^{[2]}$, $dW^{[2]}$, and $dB^{[2]}$ in the back prop
• Update the $W$ and $B$ parameters for the new layer in each iteration

Here's what it looks like:

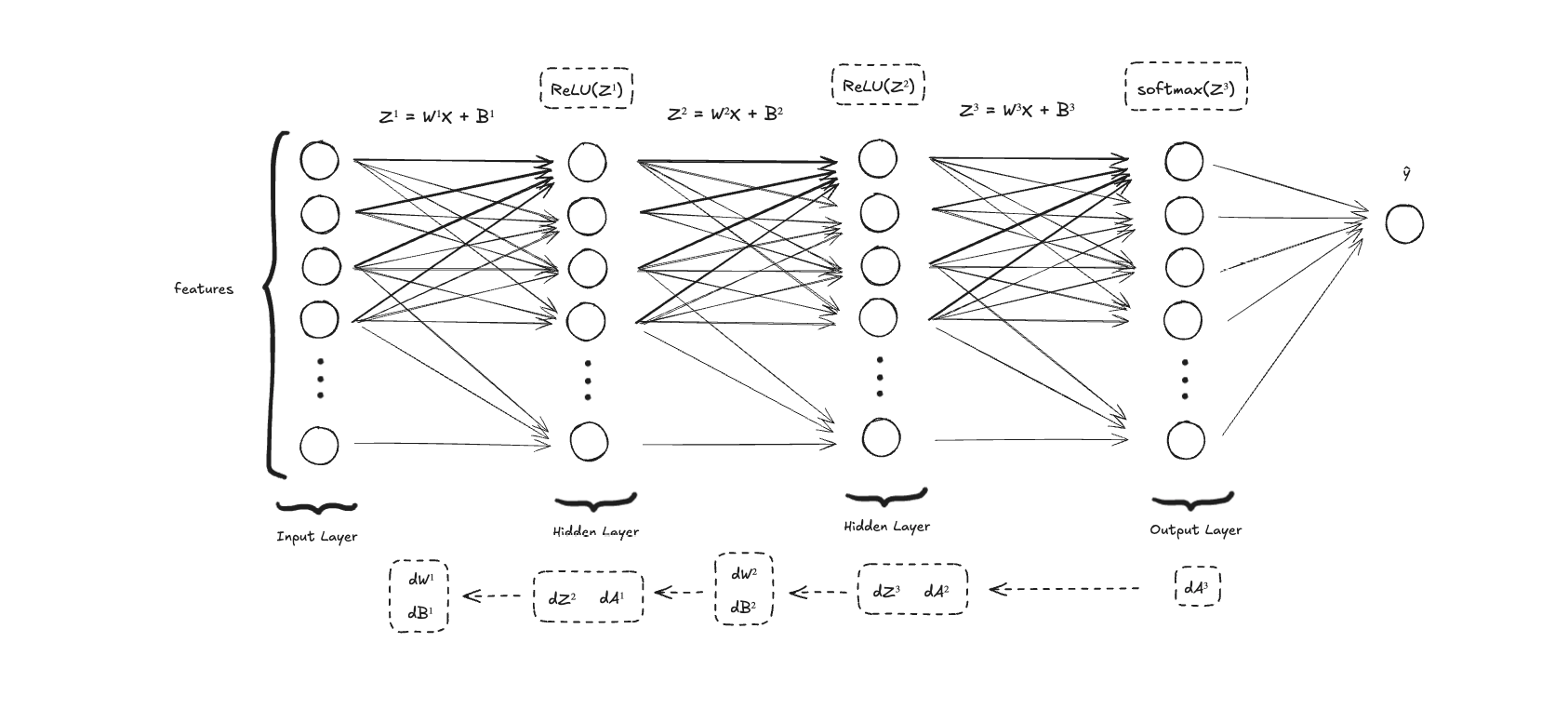
The first part initializes the $W$ and $B$ parameters for this new layer. Before we had $B^{[1]}$, $W^{[1]}$, $B^{[2]}$, and $W^{[2]}$. Now we need $B^{[3]}$ and $W^{[3]}$ but with a few adjustments because $B^{[3]}$ and $W^{[3]}$ will be the parameters for the output layer and $B^{[2]}$ and $W^{[2]}$ will be the new parameters.

def init_params():
  W1 = np.random.randn(100, 784) * np.sqrt(2 / 784)
  B1 = np.zeros((100, 1))
  W2 = np.random.randn(100, 100) * np.sqrt(2 / 10)
  B2 = np.zeros((100, 1))
  W3 = np.random.randn(10, 100) * np.sqrt(2 / 10)
  B3 = np.zeros((10, 1))
  return W1, B1, W2, B2, W3, B3

With this current implementation, the number of hidden units per layer is still fixed. In this case, we need to manually change the number of units here if we want to test a different number of hidden units.

Later on, we'll discuss a better approach for this problem, where we can abstract all this code into a class and be able to pass the number of layers and hidden units.

With the initialization of parameters, we can modify the forward propagation and apply a ReLU function for the new hidden layer. This is how it would work out:

• Compute the linear combination for the input layer
• Apply the ReLU activation function to this linear combination
• Use the output of the previous layer as the input to compute a new linear combination
• Apply the ReLU function again
• Use the output of the previous layer as the input to compute a new linear combination
• And finally, apply the softmax function to get the model output

The following modified code handles all of these operations:

def forward_propagation(W1, B1, W2, B2, W3, B3, X):
  Z1 = W1.dot(X) + B1
  A1 = ReLU(Z1)
  Z2 = W2.dot(A1) + B2
  A2 = ReLU(Z2)
  Z3 = W3.dot(A2) + B3
  A3 = softmax(Z3)
  return Z1, A1, Z2, A2, Z3, A3

Now that we have the linear combinations and outputs generated from the forward propagation process, we can modify the backward propagation to compute the derivatives ($dW$s, $dB$s) and then use them to update the parameters.

Just to recap, the back prop implementation from the shallow neural net looks like this:

def backward_propagation(Z1, A1, Z2, A2, W1, W2, X, Y):
  dZ2 = A2 - Y
  dW2 = 1 / m * dZ2.dot(A1.T)
  dB2 = 1 / m * np.sum(dZ2)

  dZ1 = W2.T.dot(dZ2) * derivative_of_ReLU(Z1)
  dW1 = 1 / m * dZ1.dot(X.T)
  dB1 = 1 / m * np.sum(dZ1)

  return dW1, dB1, dW2, dB2

We need to compute the derivatives of each layer's weights, biases, and linear combinations.

But as we can imagine, we only compute the derivatives for two layers: the output and one hidden layer. With a new hidden layer, we need to compute the derivative for a new one.

Here's the implementation:

def backward_propagation(Z1, A1, Z2, A2, Z3, A3, W1, W2, W3, X, Y):
  dZ3 = A3 - Y
  dW3 = 1 / m * dZ3.dot(A2.T) + W3
  dB3 = 1 / m * np.sum(dZ3)

  dZ2 = W3.T.dot(dZ3) * derivative_of_ReLU(Z2)
  dW2 = 1 / m * dZ2.dot(A1.T) + W2
  dB2 = 1 / m * np.sum(dZ2)

  dZ1 = W2.T.dot(dZ2) * derivative_of_ReLU(Z1)
  dW1 = 1 / m * dZ1.dot(X.T) + W1
  dB1 = 1 / m * np.sum(dZ1)

  return dW1, dB1, dW2, dB2, dW3, dB3

Because we apply a ReLU function to the first layers, their computations look similar in the back prop. We need to derive the ReLU function and generate the $dW$s and $dB$s for both of them.

With all the $dW$s and $dB$s, we now can update the $W$ and $B$ parameters.

def update_params(W1, B1, W2, B2, W3, B3, dW1, dB1, dW2, dB2, dW3, dB3, LR):
  W1 = W1 - LR * dW1
  B1 = B1 - LR * dB1
  W2 = W2 - LR * dW2
  B2 = B2 - LR * dB2
  W3 = W3 - LR * dW3
  B3 = B3 - LR * dB3
  return W1, B1, W2, B2, W3, B3

With all the modified code to support a new layer, we can now just update the gradient descent code to use the new parameters:

def gradient_descent(X, Y, LR, iterations):
  W1, B1, W2, B2, W3, B3 = init_params()
  one_hot_Y = one_hot(Y)

  for i in range(iterations + 1):
    Z1, A1, Z2, A2, Z3, A3 = forward_propagation(W1, B1, W2, B2, W3, B3, X)
    dW1, dB1, dW2, dB2, dW3, dB3 = backward_propagation(Z1, A1, Z2, A2, Z3, A3, W1, W2, W3, X, one_hot_Y)
    W1, B1, W2, B2, W3, B3 = update_params(W1, B1, W2, B2, W3, B3, dW1, dB1, dW2, dB2, dW3, dB3, LR)

    if i % 10 == 0:
      print("Iteration: ", i)
      predictions = get_predictions(A3)
      print(get_accuracy(predictions, Y))

    return W1, B1, W2, B2, W3, B3

First abstraction: neural network class

The first step I took to make the neural network more reusable was to move the code to a class so I could simply instantiate the neural net as an object and call gradient descent like this:

LR = 0.1
ITERATIONS = 3000

nn = NeuralNetwork(X_train, Y_train, X_test, Y_test, LR, ITERATIONS)
train, test = nn.gradient_descent()

We pass the training and test data, the learning rate LR, and the number of iterations for the gradient descent.

The process of moving the code to a class in Python is pretty simple, we just need to:

• Create methods with a self ”parameter”
• Initialize the parameters in the __init__ method
• Store variables in the class with self so we can reuse them in any method inside the class

Let's start with the class initialization:

class NeuralNetwork:
  def __init__(self, X_train, Y_train, X_test, Y_test, LR, iterations):
    self.X_train = X_train
    self.Y_train = Y_train
    self.Y_one_hot = self.one_hot(Y_train)
    self.X_test = X_test
    self.Y_test = Y_test
    self.LR = LR
    self.iterations = iterations
    self.init_params()

The idea here is to receive the data and the hyperparameters (LR and iterations) and store them in reusable variables. Then, we initialize the parameters $B$s and $W$s using the initi_params method:

def init_params(self):
  self.W1 = np.random.randn(100, 784) * 0.01
  self.B1 = np.zeros((100, 1))
  self.W2 = np.random.randn(100, 100) * 0.01
  self.B2 = np.zeros((100, 1))
  self.W3 = np.random.randn(10, 100) * 0.01
  self.B3 = np.zeros((10, 1))

  self.Z1 = None
  self.Z2 = None
  self.Z3 = None
  self.A1 = None
  self.A2 = None
  self.A3 = None

  self.dW1 = None
  self.dB1 = None
  self.dW2 = None
  self.dB2 = None
  self.dW3 = None
  self.dB3 = None

We also need to initialize the linear combinations ($Z$s), outputs from activation functions ($A$s), and the derivatives of $W$ and $B$ ($dW$ and $dB$). We need that to hold the values in each iteration so we can reuse them in any place in the class.

One missing part of the initialization is the one_hot method:

def one_hot(self, Y):
  one_hot_Y = np.zeros((Y.size, Y.max() + 1))
  one_hot_Y[np.arange(Y.size), Y] = 1
  return one_hot_Y.T

This is pretty much the same implementation we had before but now in a class method.

Before moving to the algorithm, let's just add the helper methods for ReLU, the derivative of ReLU, softmax, and get the prediction and accuracy:

def ReLU(self, Z):
  return np.maximum(Z, 0)

def derivative_of_ReLU(self, Z):
  return Z > 0

def softmax(self, Z):
  expZ = np.exp(Z - np.max(Z, axis=0, keepdims=True))
  return expZ / np.sum(expZ, axis=0, keepdims=True)

def get_predictions(self, A):
  return np.argmax(A, 0)

def get_accuracy(self, predictions, Y):
  return np.sum(predictions == Y) / Y.size

def predict(self, X):
  self.forward_propagation(X)
  return self.get_predictions(self.A3)

It follows the same idea of the one_hot method: pretty much the same implementation as before but now wrapped into class methods.

To do the forward propagation, we should store the linear combinations $Z$s and outputs $A$s into the class variables using self. Besides that, the implementation looks the same:

def forward_propagation(self, X):
  self.Z1 = self.W1.dot(X) + self.B1
  self.A1 = self.ReLU(self.Z1)

  self.Z2 = self.W2.dot(self.A1) + self.B2
  self.A2 = self.ReLU(self.Z2)

  self.Z3 = self.W3.dot(self.A2) + self.B3
  self.A3 = self.softmax(self.Z3)

Before, we needed to always pass the $W$s and $B$s for the function, but now we can access them using the variables defined in the self.

The backward propagation follows the same idea: we don't need to pass any parameter to the method, it directly accesses the variables inside the method:

def backward_propagation(self):
  self.dZ3 = self.A3 - self.Y_one_hot
  self.dW3 = 1 / m * self.dZ3.dot(self.A2.T) + self.W3
  self.dB3 = 1 / m * np.sum(self.dZ3)

  self.dZ2 = self.W3.T.dot(self.dZ3) * self.derivative_of_ReLU(self.Z2)
  self.dW2 = 1 / m * self.dZ2.dot(self.A1.T) + self.W2
  self.dB2 = 1 / m * np.sum(self.dZ2)

  self.dZ1 = self.W2.T.dot(self.dZ2) * self.derivative_of_ReLU(self.Z1)
  self.dW1 = 1 / m * self.dZ1.dot(self.X_train.T) + self.W1
  self.dB1 = 1 / m * np.sum(self.dZ1)

After doing forward and back, we just need to update the parameters:

def update_params(self):
  self.W1 = self.W1 - self.LR * self.dW1
  self.B1 = self.B1 - self.LR * self.dB1

  self.W2 = self.W2 - self.LR * self.dW2
  self.B2 = self.B2 - self.LR * self.dB2

  self.W3 = self.W3 - self.LR * self.dW3
  self.B3 = self.B3 - self.LR * self.dB3

The last part of the algorithm is to implement the gradient descent method and use all of the methods implemented above:

def gradient_descent(self):
  train = []
  test = []

  for i in range(self.iterations + 1):
      self.forward_propagation(self.X_train)
      self.backward_propagation()
      self.update_params()

      training_predictions = self.get_predictions(self.A3)
      training_accuracy = self.get_accuracy(training_predictions, self.Y_train)
      test_predictions = self.predict(self.X_test)
      test_accuracy = self.get_accuracy(test_predictions, self.Y_test)

      train.append(training_accuracy)
      test.append(test_accuracy)

      if i % 10 == 0:
          print("Iteration: ", i)
          print(training_accuracy)

    return train, test

It just needs to call the methods one at a time, in each iteration, and they will handle each part of the algorithm by themselves.

Dynamic number of layers and hidden units

To improve the implementation, I wanted to be able to dynamically pass the number of layers and hidden units per layer, and the neural net should figure out how to handle that.

One possible approach to pass this information to neural net model looks like this:

LR = 0.1
ITERATIONS = 3000
layer_dimensions = [784, 100, 100, 10]

nn = NeuralNetwork(X_train, Y_train, X_test, Y_test, LR, ITERATIONS, layer_dimensions)
train, test = nn.gradient_descent()

We have a layer_dimensions array and it has all the information needed.

• The length of the array is the number of layers, from the input to hidden to output layers
• In each bucket of the array will hold the number of hidden units
• 784 to map the digits, 100 for the hidden layers, and 10 to work with the softmax algorithm

Passing only this array of information, the neural net should figure out a way to work with these numbers of layers and units.

To build the neural network in this way, we need to think about dynamic layers. In other words, it will be an array and because of that, all the parameters, linear combinations, and outputs should also be arrays. That way, each place in the array will hold the value that represents the parameter for a given layer.

Let's see an example. For a 3-layer neural net, we have the input layer, two hidden layers, and one output layer, so the layer_dimensions should be something like [784, 100, 100, 10].

For the $W$ parameter, we have:

len(W) # 4

W[0] # weight vector for the input layer (usually None)
W[1] # weight vector for the first hidden layer
W[2] # weight vector for the second hidden layer
W[3] # weight vector for the output layer

Based on the layer_dimensions, we should initialize this parameter in an array format, so we hold the value for each layer.

We should have the same implementation for the bias ($B$s), the linear combinations ($Z$s), and the output generated by the activation function ($A$s).

Let's focus on the weight and bias first and then we can implement the same idea for the rest too.

The fixed approach can be hardcoded, meaning the weights and biases will be directly set on their own variable, so there's no need for an array to represent each layer.

To recap, here's the fixed version implementation:

def init_params(self):
  self.W1 = np.random.randn(100, 784) * 0.01
  self.B1 = np.zeros((100, 1))
  self.W2 = np.random.randn(100, 100) * 0.01
  self.B2 = np.zeros((100, 1))
  self.W3 = np.random.randn(10, 100) * 0.01
  self.B3 = np.zeros((10, 1))

This is how the weights and biases are created:

• W1 should have the number of hidden units (100) per value of the input (784)
• W2 should have the number of hidden units (100) per size of the previous layer (100)
• W3 should have the number of hidden units (10) per size of the previous layer (100)
• $Z^{[1]}$, B2, and B3 should have the number of hidden units per 1

If these rules, we have the logic:

def init_params(self, layer_dimensions):
  self.W = [None]
  self.B = [None]

  for l in range(1, len(layer_dimensions)):
    current_layer_dimension = layer_dimensions[l]
    previous_layer_dimension = layer_dimensions[l - 1]
    w = np.random.randn(current_layer_dimension, previous_layer_dimension) * 0.01
    b = np.random.randn(current_layer_dimension, 1)
    W.append(w)
    B.append(b)

First, we need to create the array for the weights and biases. The first elements of both arrays are None because the input layer doesn't have weights and biases.

Then, we need to iterate through the layer_dimensions from 1 to the last one. We already have the first weights and biases and starting from 1, we can get the previous layer dimension to build the current weight. Biases need only the current layer dimension.

Now we need to implement the same idea for the linear combinations, layer outputs, and derivatives.

self.Z = [None for i in range(len(layer_dimensions))]
self.Z_test = [None for i in range(len(layer_dimensions))]
self.A = [X_train] + [None for i in range(len(layer_dimensions) - 1)]
self.A_test = [X_test] + [None for i in range(len(layer_dimensions) - 1)]
self.dZ = [None for i in range(len(layer_dimensions))]
self.dW = [None for i in range(len(layer_dimensions))]
self.dB = [None for i in range(len(layer_dimensions))]

The idea here is simpler because we don't need to calculate anything. For linear combinations and derivatives, we only need to initialize them with null values (or None in Python).

Layer outputs are almost the same, but the first value is actually the dataset. We have $A$ for the training data and A_test for the test data. The following values in these arrays will be the output of each layer until the end of the neural net.

After have the parameters initialization in place, we need to adjust the implementation of the forward and backward propagations again. Let's recap what the implementation looked like:

def forward_propagation(self, X):
  self.Z1 = self.W1.dot(X) + self.B1
  self.A1 = self.ReLU(self.Z1)

  self.Z2 = self.W2.dot(self.A1) + self.B2
  self.A2 = self.ReLU(self.Z2)

  self.Z3 = self.W3.dot(self.A2) + self.B3
  self.A3 = self.softmax(self.Z3)

def backward_propagation(self):
  self.dZ3 = self.A3 - self.Y_one_hot
  self.dW3 = 1 / m * self.dZ3.dot(self.A2.T) + self.W3
  self.dB3 = 1 / m * np.sum(self.dZ3)

  self.dZ2 = self.W3.T.dot(self.dZ3) * self.derivative_of_ReLU(self.Z2)
  self.dW2 = 1 / m * self.dZ2.dot(self.A1.T) + self.W2
  self.dB2 = 1 / m * np.sum(self.dZ2)

  self.dZ1 = self.W2.T.dot(self.dZ2) * self.derivative_of_ReLU(self.Z1)
  self.dW1 = 1 / m * self.dZ1.dot(self.X_train.T) + self.W1
  self.dB1 = 1 / m * np.sum(self.dZ1)

We can see that the number of layers is fixed and not dynamic. The idea of transforming fixed layers into dynamic ones is to iterate through the layer_dimensions and update linear combinations, layer outputs, and derivatives appropriately.

Let's see the forward prop first:

def _is_last_layer(self, layer):
  return layer == len(self.layer_dimensions) - 1

def forward_propagation(self):
  for layer in range(1, len(self.layer_dimensions)):
    self.Z[layer] = self.W[layer].dot(self.A[layer - 1]) + self.B[layer]

    if self._is_last_layer(layer):
      self.A[layer] = self.softmax(self.Z[layer])
    else:
      self.A[layer] = self.ReLU(self.Z[layer])

Here's the algorithm:

• Iterate through the layer_dimensions, starting from 1 because we don't need to compute linear combinations nor layer outputs for the input layer
• In each layer, we should update the linear combination ($Z$) and the layer output ($A$)
• For the linear combination, notice that we need to access the output from the previous layer
  • For the first hidden layer, the output of the previous layer is the input data
  • For the following layers, the data is the output generated by the previous layer
• For the layer output, we first need to check if it's the last layer or not
  • If it is, we should use softmax
  • If it's not, we should use ReLU

The backpropagation looks pretty similar to this previous implementation. But we need to iterate from the last layer to the first one.

def backward_propagation(self):
  for layer in range(len(self.layer_dimensions) - 1, 0, -1):
    if self._is_last_layer(layer):
      self.dZ[layer] = self.A[layer] - self.Y_one_hot
    else:
      self.dZ[layer] = self.W[layer + 1].T.dot(self.dZ[layer + 1]) * self.derivative_of_ReLU(self.Z[layer])

    self.dW[layer] = 1 / m * self.dZ[layer].dot(self.A[layer - 1].T) + self.W[layer]
    self.dB[layer] = 1 / m * np.sum(self.dZ[layer])

Let's unpack the algorithm for backprop:

• First, we iterate through the layer_dimensions but now backward, from the last layer to the first one
• If it is the last layer, we should compute the derivative of softmax and update the derivative of the linear combination
• If it is not, we compute the derivative of ReLu and update the derivative of the linear combination
• And finally compute the derivative of the weights and biases

The last two parts missing are the parameters update and how we should modify the predict method to support the new array style for layers.

The parameters update is fairly easy. Using the same idea of iterating through the array, we should modify it very fast.

This is the fixed version:

def update_params(self):
  self.W1 = self.W1 - self.LR * self.dW1
  self.B1 = self.B1 - self.LR * self.dB1

  self.W2 = self.W2 - self.LR * self.dW2
  self.B2 = self.B2 - self.LR * self.dB2

  self.W3 = self.W3 - self.LR * self.dW3
  self.B3 = self.B3 - self.LR * self.dB3

And here it's the dynamic version:

def update_params(self):
  for layer in range(1, len(self.layer_dimensions)):
    self.W[layer] = self.W[layer] - self.LR * self.dW[layer]
    self.B[layer] = self.B[layer] - self.LR * self.dB[layer]

The predict method should work similarly to the forward propagation but the difference here is the fact that it will be working on top of the test dataset rather than the training dataset.

def predict(self):
  for layer in range(1, len(self.layer_dimensions)):
    self.Z_test[layer] = self.W[layer].dot(self.A_test[layer - 1]) + self.B[layer]

    if self._is_last_layer(layer):
      self.A_test[layer] = self.softmax(self.Z_test[layer])
    else:
      self.A_test[layer] = self.ReLU(self.Z_test[layer])

  return self.get_predictions(self.A_test[-1])

It moves forward in each layer, starting with the test dataset, passing through activation functions like ReLU and then softmax, and finally the the prediction for the output of the last layer (output layer).

With that, we finalized the dynamic approach, now we can use how many layers and hidden units we want. I tested the neural net with 10 layers and it worked out. But the performance was not the best one. Let's talk about it in the next section.

Model Optimizations

When testing the neural network model with 3 layers, I noticed a significant performance issue. The model only reached around 20% accuracy, and with each additional training iteration, the performance started to deteriorate rather than improve.

That seems to be a very common challenge in deep neural networks and points to several underlying issues that need to be addressed. To improve the model's performance, I focused on two key optimizations I'm going to cover in this post:

• Weight Initialization: The model was suffering from the vanishing (shrinking exponentially) and exploding (growing uncontrollably) gradients problem, where the gradients become either too small or too large as they propagate through the layers. Proper weight initialization can help mitigate this issue.
• Regularization: The model was overfitting the training data, leading to poor generalization. Adding regularization helped control the model's complexity and improve its ability to generalize.

I also experimented with replacing ReLU with the Leaky ReLU Activation function. But better weight initialization and regularization were sufficient to make the model perform way better, so I won't lose much time covering Leaky ReLU in this post.

Let's first focus on the vanishing/exploding gradients problem and see the solution that got a better model performance.

The vanishing and exploding gradients problem happens because the gradients become very large or very small. And that happens with the increase of layers in deep neural networks. In other words, the deeper the model, the smaller/larger the gradients.

Let's recap how the math of neural nets works before giving the intuition on why the gradients become too large or too small with deeper layers.

As an example, we have a neural network with 3 layers, and these are the linear combinations of each layer:

The $X$ for the first layer is the input data. The $X$ for the second and third layers are the output from the previous layer (linear combination with applied activation function).

With the activation function, we get $A$, so it looks like this:

And then we can replace the X for the second and third layers like this:

To sum up, we can say that the output is:

Now let's understand the intuition behind why gradients explode or vanish with the increase of layers in deep neural networks.

For the sake of simplicity, let's say that $B = 0$ and $g(Z) = Z$.

This:

will become this:

The output of the activation function will also be only Z for simplicity. So:

Because we simplified the math, we get the output as

Suppose W is a simple vector like

The output will be 1.5^[l-1]. The deeper the neural net, the larger the output will be. In other words, with the increase in the number of layers in the model, the output will increase exponentially and explode.

If $W$ is

Then, the output is $0.5^{[l-1]}$ and will vanish with the increase of layers.

One of the ways to minimize this problem is choosing a better weight initialization value. This is how a good weight initialization helps: Well-chosen initialization techniques, such as Xavier/Glorot initialization or He initialization, aim to keep the signal flowing smoothly through the network's layers, preventing gradients from vanishing or exploding.

Besides that, it also helps with:

• Faster Convergence: By starting the training process in a more promising region of the weight space, good initialization can significantly speed up convergence.
• Improved Generalization: Proper initialization can help the network explore a wider range of solutions during training, increasing the likelihood of finding a good global minimum and improving its ability to generalize to new, unseen data.

In our model, we use the He initialization, a weight initialization technique specifically designed for neural networks that use the ReLU activation function. it helps with the vanishing/exploding gradients problem by making the weights not much bigger than 1 and not much smaller than 1.

In practice, we just need to add this term $\sqrt{\frac{2}{n^{[l-1]}}}$ to the weight initialization, where $n^{[l-1]}$ is the number of units in the previous layer.

In the Python implementation, it works pretty simple:

w = np.random.randn(current_layer_dimension, previous_layer_dimension) * np.sqrt(2 / previous_layer_dimension);

I just added the np.sqrt(2 / previous_layer_dimension) term to the weight initialization.

With better weight initialization, the performance on the training data was hitting 96% accuracy. But it was overfitting, in other words, great performance on the training data but not on unseen/test data.

One of the ways we could fix this problem is by adding a regularization term to the learning process of the neural net and hoping it will generalize better.

The idea is that regularization adds a penalty term to the model's loss function. This penalty discourages the model from having excessively large weights. By keeping the weights smaller, the model becomes simpler and less prone to overfitting.

One piece of intuition on why regularization helps with reducing overfitting is the fact that if we zero some of the hidden units reduces the impact of some of the hidden units (smaller effect) and the neural network becomes simpler and smaller and it tend to generalize better.

The implementation is also pretty simple. We should just add the regularization term to the weights. There are two possibilities:

1. In the parameters update or;
2. In the computation of the derivative of the weights

In this implementation, I added it to the second approach and it worked out well.

self.dW[layer] = 1 / m * self.dZ[layer].dot(self.A[layer - 1].T) + (lambda_reg / m) * self.W[layer]

lambda_reg is the regularization term with a default 0.01.

Here's the full implementation for the backward propagation:

def backward_propagation(self, lambda_reg=0.01):
  for layer in range(len(self.layer_dimensions) - 1, 0, -1):
    if self._is_last_layer(layer):
      self.dZ[layer] = self.A[layer] - self.Y_one_hot
    else:
      self.dZ[layer] = self.W[layer + 1].T.dot(self.dZ[layer + 1]) * self.derivative_of_LeakyReLU(self.Z[layer])

    self.dW[layer] = 1 / m * self.dZ[layer].dot(self.A[layer - 1].T) + (lambda_reg / m) * self.W[layer]
    self.dB[layer] = 1 / m * np.sum(self.dZ[layer])

Future Topics & Implementations

In this post, I covered a lot of topics and implementations, but I still have some interesting ideas I can write about in the following post.

Here are these ideas:

• Input Normalization
• Mini Batch
• Momentum, Adam, and Exponentially Weighted Averages

These are fascinating topics to learn and implement from scratch in the model. They are topics for a future post.

Until then.

Resources

• Mathematics for Machine Learning
• Machine Learning Research
• Building A Neural Network from Scratch with Mathematics and Python

Twitter · Github